Symphony Math® explicitly teaches foundational number sense skills - the basis of all higher level mathematics. The program supports a year 1-8 math curriculum, as well as providing a highly supportive interface for students needing help with math, including older students.
Symphony Math® helps students to understand the deeper mathematical meaning and not merely repeat answers by rote. Concept Stages (1-26) automatically adjust based on each students answers to provide more support or practice where needed, or students can click for a hint. Extra paper based practice sheets are also available.
After completing the concepts stages, students in year 6 and above are further challenged with skills practice tasks on higher order math concepts such as geometry and statistics.
Manipulative Example
Symphony Math Dot Cards help to teach the math concept 'subitising'
Symphony Math® uniquely designed delivery methods ensure that students – regardless of learning styles or knowledge levels – fully grasp fundamental mathematical ideas, even for difficult-to-explain and abstract concepts.
Stages of Symphony Math Development
A tightly connected progression forms the conceptual sequence of Symphony Math®. These underlying “big ideas” provide the foundation for mathematical learning. As students master each big idea before moving on to the next, they learn to succeed with more complicated math later on.Concepts Stages 26 program stages covering foundational number sense. | |||||
Year 1 | Year 2 | Year 3 | Year 4 | Year 5 | Year 6 |
|
|
|
|
|
|
Fact Fluency Timed practice rounds that are introduced throughout. | |||||
Fact Fluency +- to 5 | Fact Fluency +- to 20 | Fact Fluency +- with Tens | Fact Fluency X÷ to 100 | Fact Fluency X÷ with Tens | Fact Fluency X÷ with Tens |
Skills Practice (Year 6-8 skill level) 15+ additional program stages with practice tasks. | |||||
|
| ||||
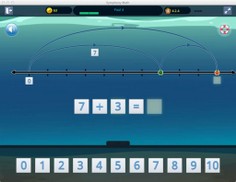
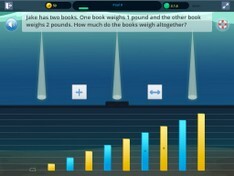
All students start at Stage 1 of the program, however those who demonstrate mastery early on in each Stage will progress rapidly to the next Stage. In this way the program ensures there are no critical gaps in learning that will prevent mastery of more difficult math concepts. After each online program Stage, the program will automatically prompt students to have a go at writing their own examples of what they have just learned on paper. These Symphony 'Checkpoints' help cement learning. Students receive other prompts to create models in their journals as they use Symphony Math, especially when they show signs of struggle with a particular concept or visual model. Multiple Ways of Knowing Number concepts are practiced using multiple "Ways of Knowing" which help students visualise, reinforce, and apply ideas quickly and accurately. Students use visual models and manipulatives such as: Counting Bars, Dot Cards, Number Lines, Number Problems, Word Problems, Fraction Bars and Auditory Problem Solving. Visual models are critical for math instruction and learning as evidenced by brain research such as Six distinct activity environments provide multiple representations of each concept. | |
Manipulatives: |
|
Manipulatives and Symbols |
|
Symbols |
|
Story Problems |
|
Mastery Round |
|
Instructive Feedback
Instructive feedback encourages independent thinking by revealing the nature of each incorrect response. For example, if a student answers 3 + 2 = ? with a 6, the program immediately shows that a 2 bar combined with a 3 bar is not the same length as a 6 bar.
This approach helps students deduce for themselves why an answer is incorrect.
Built in ‘help’
The "Help" button provides clues that leads the student closer to working out the solution for themselves.
This helps students develop long-lasting problem solving skills and reduce their dependence on technology for solutions.
Individualised learning
If students are struggling the Symphony Math® program slows progress until the student achieves the necessary understanding. This allows students to learn at their own levels.
As students’ progress through the program, practice worksheets are available as extra pen and paper practice to reinforce their online learning. Extension Worksheets are also available at the completion of each level upon request.
Symphony Math runs on Mac or Windows computers, iPads, and Chromebooks or Chrome Touchscreens meeting specifications.
